C2-排序算法总结

2017-08-02

1 对比分析图

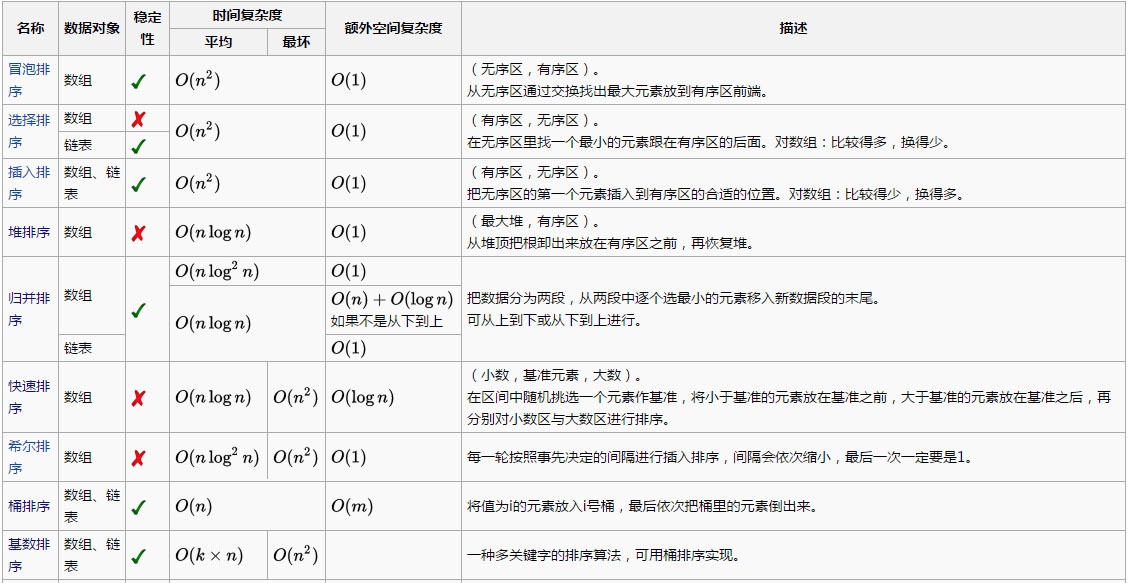
均按从小到大排列
k代表数值中的”数位”个数
n代表数据规模
m代表数据的最大值减最小值

稳定性：稳定排序算法会让原本有相等键值的纪录维持相对次序。也就是如果一个排序算法是稳定的，当有两个相等键值的纪录R和S，且在原本的列表中R出现在S之前，在排序过的列表中R也将会是在S之前。

2 算法原理及实现

2.1 冒泡排序

概述

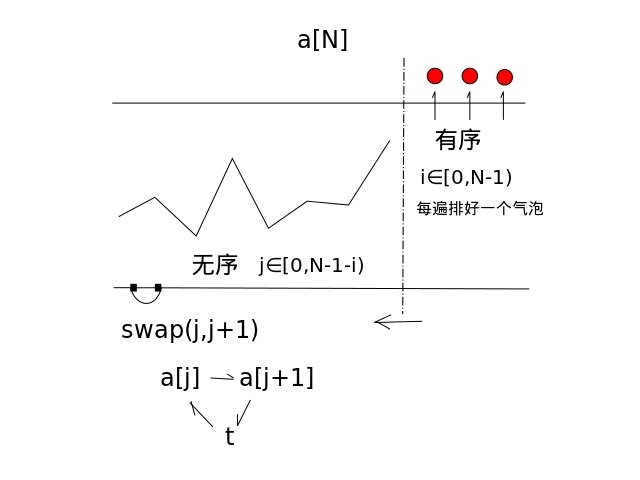
冒泡排序通过重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来，直到没有再需要交换的元素为止（对n个项目需要O(n^2)的比较次数）。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

实现步骤

比较相邻的元素。如果第一个比第二个大，就交换他们两个。　
对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

性能

最差时间复杂度 O(n^2)
最优时间复杂度 O(n)　
平均时间复杂度 O(n^2)
最差空间复杂度总共O(n)，需要辅助空间O(1)

代码实现

/**
 * 优化版冒泡排序
 * 思路:每次冒泡都会将无序部分最大的数移动到无序部分的最后一个位置
 * @author NikoBelic
 * @create 16/01/2017 17:54
 */
public static int[] sort(int[] array)
{
    boolean swap = false;
    for (int i = 0; i < array.length - 1; i++)
    {
        swap = false;
        for (int j = 0; j < array.length - i - 1; j++)
        {
            if (array[j] > array[j + 1])
            {
                int t = array[j];
                array[j] = array[j + 1];
                array[j + 1] = t;
                swap = true; // 如果某一轮冒泡发现没有任何位置的交换,那么说明这个数组已经是有序的,无需再进行下一轮冒泡
            }
        }
        if (!swap)
            break;
    }
    return array;

2.2 简单选择排序

概述

设所排序序列的记录个数为n，i　取　1,2,…,n-1　。
从所有n-i+1个记录（Ri,Ri+1,…,Rn）中找出排序码最小（或最大）的记录，与第i个记录交换。执行n-1趟后就完成了记录序列的排序。

以排序数组｛3，2，1，4，6，5｝为例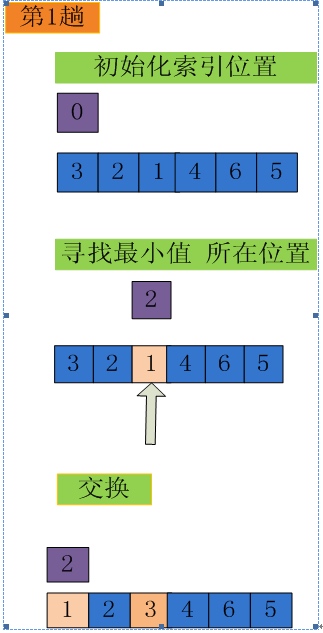

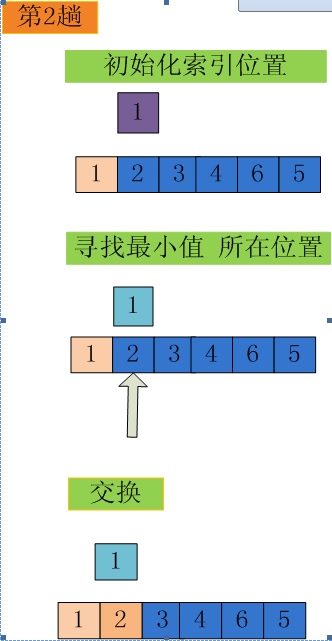
简单选择排序性能

在简单选择排序过程中，所需移动记录的次数比较少。最好情况下，即待排序记录初始状态就已经是正序排列了，则不需要移动记录。　
最坏情况下，即待排序记录初始状态是按第一条记录最大，之后的记录从小到大顺序排列，则需要移动记录的次数最多为3（n-1）。

简单选择排序过程中需要进行的比较次数与初始状态下待排序的记录序列的排列情况无关。
当i=1时，需进行n-1次比较；当i=2时，需进行n-2次比较；依次类推，共需要进行的比较次数是(n-1)+(n-2)+…+2+1=n(n-1)/2，即进行比较操作的时间复杂度为O(n^2)，进行移动操作的时间复杂度为O(n)。　

简单选择排序是不稳定排序。

/**
 * 简单选择排序
 * 思路:每次循环都将无序数组的第一个元素和无序数组中的最小元素互换位置
 * @author NikoBelic
 * @create 17/01/2017 13:29
 */
public static int[] sort(int[] array)
{
    int index;
    int min;
    for (int i = 0; i < array.length; i++)
    {
        index = i;
        min = array[i];
        // 找到最小值
        for (int j = i; j < array.length; j++)
        {
            if (array[j] < min)
            {
                min = array[j];
                index = j;
            }
        }
        int t = array[i];
        array[i] = array[index];
        array[index] = t;
    }
    return array;

2.3 插入排序

概述

将一个数据插入到已经排好序的有序数据中，从而得到一个新的、个数加一的有序数据，算法适用于少量数据的排序，是稳定的排序方法。

插入排序又分为　直接插入排序　和 折半插入排序。

直接插入排序

把待排序的纪录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的纪录插入完为止，得到一个新的有序序列。

代码实现

/**
* 普通插入排序   空间复杂度O(1) 时间复杂度O(n^2)
* 思路:从第2个元素开始,与其左边的有序数组进行逐一比较,找到其需要正确插入的位置
* 将该位置右边的数组向右移动一位,然后将当前元素插入进去
*
* @Author NikoBelic
* @Date 16/01/2017 09:36
*/
public static int[] sort(int[] array)
    {
        int key; // Insert value
        int preIndex; // index that need to be move
        for (int i = 1; i < array.length; i++)
        {
            key = array[i]; // get the insert value
            preIndex = i - 1;
            // move elements which less than key
            while (preIndex >= 0 && key < array[preIndex])
            {
                array[preIndex + 1] = array[preIndex];
                preIndex--;
            }
            // put the key in the correct position
            array[preIndex + 1] = key;
        }
        return array;
    }

效率分析

空间复杂度O(1) 　
　　
平均时间复杂度O(n^2)

最差情况：反序，需要移动n*(n-1)/2个元素，运行时间为O(n^2)。
　　
最好情况：正序，不需要移动元素，运行时间为O(n)．

折半插入排序

直接插入排序中要把插入元素与已有序序列元素依次进行比较，效率非常低。　
　　
折半插入排序,使用使用折半查找的方式寻找插入点的位置, 可以减少比较的次数,但移动的次数不变, 时间复杂度和空间复杂度和直接插入排序一样，在元素较多的情况下能提高查找性能。

代码实现

/**
 * 折半插入排序 空间、时间复杂度不变,较少了比较次数
 *
 * @Author NikoBelic
 * @Date 16/01/2017 09:37
 */
public static int[] binarySort(int[] array)
{
    //从数组的第二个位置开始遍历值
    for(int i = 1; i < array.length; i++)  {
        int key = array[i];           //暂存要插入的值
        int pre = 0;              //有序序列开始和结尾下标申明
        int last = i - 1;
        // 折半查找出插入位置 a[pre]
        while(pre <= last)  {
            int mid = (pre + last) / 2;
            if(key < array[mid])  {
                last = mid - 1;
            } else {
                pre = mid + 1;
            }
        }
        //a[i]已经取出来存放在key中，把下标从pre + 1到 i-1的元素依次后移
        for(int j = i; j >= pre + 1; j--)  {
            array[j] = array[j - 1];
        }
        //把值插入空白位置
        array[pre] = key;
    }
    return array;
}

直接插入排序是，比较一个后移一个
折半插入排序是，先找到位置，然后一起移动；

2.4 快速排序

概述

快速排序（Quicksort）是对冒泡排序的一种改进，又称划分交换排序（partition-exchange sort。
快速排序使用分治法（Divide and conquer）策略来把一个序列（list）分为两个子序列（sub-lists）。

步骤

从数列中挑出一个元素，称为”基准”（pivot）
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序

网上的通俗讲解

快速排序由于排序效率在同为O(N*logN)的几种排序方法中效率较高，因此经常被采用，再加上快速排序思想—-分治法也确实实用，因此很多软件公司的笔试面试，包括像腾讯，微软等知名IT公司都喜欢考这个，还有大大小的程序方面的考试如软考，考研中也常常出现快速排序的身影。

总的说来，要直接默写出快速排序还是有一定难度的，因为本人就自己的理解对快速排序作了下白话解释，希望对大家理解有帮助，达到快速排序，快速搞定。

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

该方法的基本思想是：

先从数列中取出一个数作为基准数。
分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
再对左右区间重复第二步，直到各区间只有一个数。

虽然快速排序称为分治法，但分治法这三个字显然无法很好的概括快速排序的全部步骤。因此我的对快速排序作了进一步的说明：挖坑填数+分治法：

先来看实例吧，定义下面再给出（最好能用自己的话来总结定义，这样对实现代码会有帮助）。

以一个数组作为示例，取区间第一个数为基准数。

初始时，i = 0; j = 9; X = a[i] = 72

由于已经将a[0]中的数保存到X中，可以理解成在数组a[0]上挖了个坑，可以将其它数据填充到这来。

从j开始向前找一个比X小或等于X的数。当j=8，符合条件，将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++; 这样一个坑a[0]就被搞定了，但又形成了一个新坑a[8]，这怎么办了？简单，再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数，当i=3，符合条件，将a[3]挖出再填到上一个坑中a[8]=a[3]; j–;

数组变为：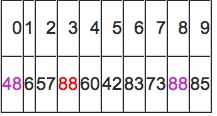

i = 3; j = 7; X=72
再重复上面的步骤，先从后向前找，再从前向后找。
从j开始向前找，当j=5，符合条件，将a[5]挖出填到上一个坑中，a[3] = a[5]; i++;
从i开始向后找，当i=5时，由于i==j退出。
此时，i = j = 5，而a[5]刚好又是上次挖的坑，因此将X填入a[5]。

数组变为：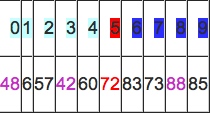

可以看出a[5]前面的数字都小于它，a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。

对挖坑填数进行总结

i =L; j = R; 将基准数挖出形成第一个坑a[i]。
j–由后向前找比它小的数，找到后挖出此数填前一个坑a[i]中。
i++由前向后找比它大的数，找到后也挖出此数填到前一个坑a[j]中。
再重复执行2，3二步，直到i==j，将基准数填入a[i]中。

实现

public static void quickSort(int[] a, int left, int right)
    {
        if (left < right)
        {
            int i = left, j = right;
            // 以中间数为基准
            //SortUtil.swap(a, left, (left + right) / 2);
            // 以随机数为基准
            SortUtil.swap(a, left, SortUtil.getRandomIndex(left, right));
            int x = a[left]; // a[left] 就是被挖出的第一个坑
            while (i < j)
            {
                // 从右向左找小于x的数来填a[i]
                while (i < j && a[j] > x)
                    j--;
                if (i < j)
                    a[i++] = a[j]; // 将a[j]填到a[i]，a[j]形成了新的坑
                // 从左向右找大于x的数来填a[j]
                while (i < j && a[i] < x)
                    i++;
                if (i < j)
                    a[j--] = a[i];// 将[i]天到a[j],a[i]形成了新的坑
            }
            a[i] = x;// 退出时，i等于j，将x填到这个坑
            quickSort(a, left, i - 1);
            quickSort(a, i + 1, right);
        }
    }

3 桶排序

时间复杂度O(n),思想都是来自于桶排序，桶排序不是一种具体的排序算法，而是一种思想。

3.1 计数排序

分别创建100-300号的桶，将待排序数按对应的桶号存储，全部存储完毕后，从100号-300号桶逐一倒出数值，即完成排序。

3.2 基数排序

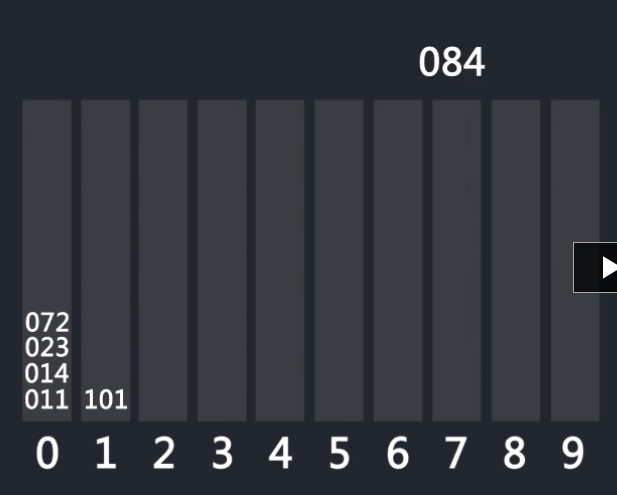
将待排序数列分别按照，个位、十位、百位添加到不同的桶中并倒出，三次装入与倒出后的数列即为有序数列。

4 排序笔试面试题

已知一个几乎有序的数组，几乎有序是值如果把数组排好顺序的话，每个元素移动的距离不超过k，并且k相对于数组长度来说很小。请问选择什么方法对其排序比较好？
- 冒泡、选择都不好，因为他们是严格的O( n^2 )算法
- 插入排序还不错，其排序过程与原始顺序有关，时间复杂度不会超过O(N*K)
- 快排、归并不好
- 答案是改进后的堆排序
  - 由于元素移动距离不会超过k，i=0,所以建立a[i,k-1]的小根堆，将最小值换到a[i],i++
  - 构建a[i,k+i]的小根堆，将当前堆最小值换到a[i],i++
  - 堆顶的弹出顺序其实就是最终排序结果
  - 每得到一个数的时间复杂度为O(logK),总共N个数，时间复杂度就是O(N*logK)
判断数组中是否有重复值。必须保证额外的空间复杂度为O(1)
- 如果没有空间复杂度的限制，用哈希表实现最好
- 有空间复杂度要求，需要先排序，然后判断（遍历一次）
- 答案是改出一个非递归版本的堆排序，堆排序递归空间复杂度是O(logN)
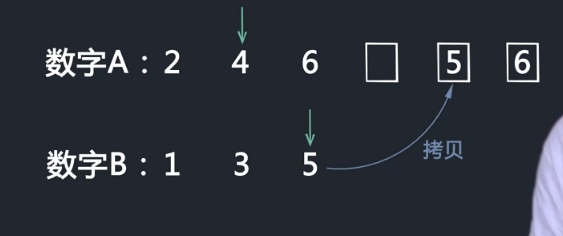
把两个有序数组合并为一个数组，第一个数组空间正好可以容纳两个数组的元素。
- 从后往前遍历数组A和B

荷兰国旗问题。只包含0，2，3的整数数组进行排序，要求使用交换、原地排序，而不是利用计数进行排序。
- 与快排的划分过程类似
- 如果当前数为1，那么就与0区的后一个数进行交换，并且0区向后扩充1
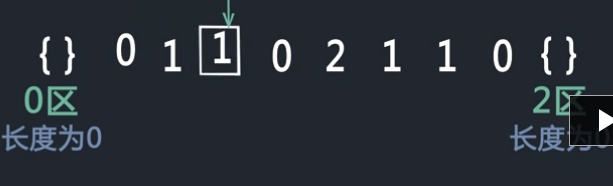
- 如果当前数是2，那么当前数与2区前一个数进行交换，并且2区向前扩充1
- 注意2区域的前一个数是我们没有遍历过的数，所以index不能加1

给定一个2维数组，在2维数组中，每一行每一列都是有序的，给定一个数k，判断2维数组中是否包含这个数。
- 如果二维数组规模为 m*n，那么最优时间复杂度为m+n
- 从2维数组右上角开始找
- 如果当前数大于k，舍弃当前列，向左移动
- 如果当前数小于k，舍弃行，向下移动
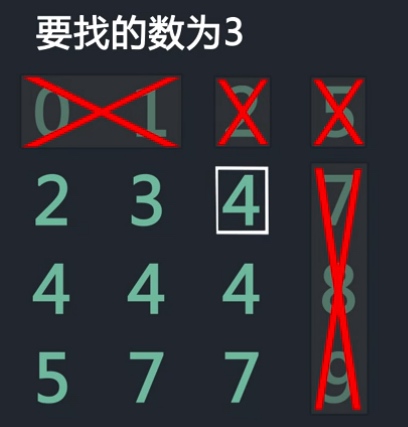
- 在查找过程中如果找到该数则返回true，若最终角标都越界了还没找到，则返回false

给定一个数组，求解数组中需要排序的最短子数组的长度。比如[1,5,4,3,2,6,7]，返回4，因为只有[5,4,3,2]需要排序
- 最优解：时间复杂度O(n),空间复杂度O(1)
- 首先从左向右遍历数组，过程中用max来标记过程中数值的最大值，并记录max>curr_val 最后出现的to_index
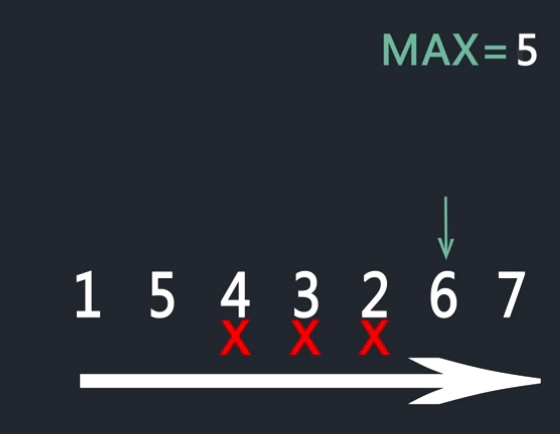
  - 从右往左遍历数组，过程中用min来标记过程中数值最小的值，并记录min<curr_val最后出现的位置from_index
  - [from_index,to_index]就是需要排序的最短子数组

给定一个无序数组a，返回如果排序之后，相邻两数的最大差值。
- 最优解O(n),空间O(n)
- 思想来自于桶排序
- 遍历数组，找到min和max，将[min,max]分为 n 个等量区间
- 同一个桶中的数差不会超过当前桶区间，所以不用考虑。
- 考虑每一个桶的最小值和上一个桶中的最大值，记录最大差值，即为答案